Logic Gates

The basic gates

There are five essential logic gates to understand. Each gate accepts some number of input signals and produces a single output signal.

The first gate is the buffer. Given a particular logic state as its input, the buffer matches that logic state at its output. For input "A" and output "Y" the logic equation is
    Y = A
This would seem to be a particularly useless logic gate since it doesn't seem to do anything, but we'll see later where this is useful.

The next gate is the AND gate. Given two or more logic state inputs, the output is "1" only if all of the inputs are "1." If any input is "0" then the output is also "0." For inputs "A" and "B," the logic equation is
    Y = A AND B
For the ouput to be "1," you must have a "1" at input A "and" input B (and any other inputs, for as many as the gate has). The AND function in binary is equivalent to multiplication.

The next gate is the OR gate. Given two or more logic state inputs, the output is "1" if any of the inputs are "1." For inputs "A" and "B," the logic equation is
    Y = A OR B
For the output to be "1," you need a "1" at input A "or" input B (or any other input).

The next gate is the exclusive-OR gate, commonly spelled as "XOR." Given two logic state inputs, the output is "1" if the inputs are at different states, or "0" if the inputs are at the same state. The logic equation is
    Y = A XOR B
For the output to be "1," you need a "1" at input A "or" input B, "exclusive" of the other.

The last essential gate is the inverter, sometimes called the "NOT" gate. Given a particular logic state as its input, the inverter presents the opposite state as its output. The logic equation is
    Y = NOT( A )
The output is the state which the input is "not."

Truth tables

For the five basic logic gates, a textual description of the operations (what output state results from various combinations of input states) is sufficient to give you an understanding of the function. But as logic gates are combined to make more complex functions, describing the behavior in English begins to get confusing. What is needed is a precise way to show the relationships between inputs and outputs. We do this by means of a "truth table."

This is simply a table of states, where we make a column for each input or output and a row for each combination of input states. From the table you can quickly see that given certain states at the inputs, a specific output state is to be expected. Here are the truth tables for the gates we covered so far:

Check these tables against your understanding of the logic gates to make sure you agree with all the output results. Of course, the basic logic gates are fairly simple. But if we want to represent something a little more complicated, a truth table helps clarify things. For example, suppose we have a circuit (made up of several logic gates) which functions as a single bit addition function. Such a function has three inputs (the two values being added, plus a carry input) and two outputs (the result for that digit, and the overflow carry). Now the truth table becomes a bit more complicated, like this:

The input combinations don't have to be in a particular order, as long as all the cases (or all the cases you care about) are represented. Notice also our use of names for the signals: A and B for the values being added, CY_-1 for the carry from the previous bit, Y for the digit output and CY for the carry to the next digit. The use of "A," "B," "C"... for input data and "Y" for output data are common name choices. The "-1" subscript on the carry input indicates that the carry is from the digit whose place value is one less. These are some naming conventions you may encounter, but the simple rule is, somewhere the meanings of these names need to be described.

A truth table may have entries besides one and zero. One example we'll offer for now is that "X" as an input state means "don't care;" that is, the state really doesn't matter. For example, we could express the AND gate truth table like this:

This truth table tells us that if A is 0, Y is zero no matter what B is, and also that if B is 0, Y is zero no matter what A is. There are other notations that may occur in a truth table which we will not encounter until later in this course.

Logic gate symbols

When we start to use basic logic gates together to perform more complex functions, we need a way to diagram the way the function works. One way to do this is to write more complex logic expressions; several hardware description languages such as VHDL, Verilog and PALASM work this way. But a more standardized approach is to draw diagrams. Each logic operation has a particular symbol used for these diagrams. 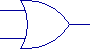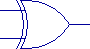The symbols for our five basic logic gates are:

Buffer	AND	OR	XOR	Inverter

The straight lines on either side of the symbols are inputs or outputs. The inputs are all shown on the left; it is a convenient convention for logic diagrams to have signals "flow" from left to right, although in fact the direction is indicated by which way the symbol points. Note also that for the AND and OR gates, there could be more than two inputs; these would be indicated by additional lines connected to the left side of the symbol.

Using these symbols, and connecting input and output lines, you have a way of representing functions made up of several gates. For example, consider this function:

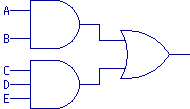
The drawing represents this expression:
    Y = (A AND B) OR (C AND D AND E)
We use straight lines to connect the gates. The "flow" of the information is from left to right because that is the way the gates are pointing, not because of their placement on the page.

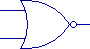
Inverted levels

We saw earlier that the symbol for an inverter is a combination of the symbol for the buffer and an open dot. Actually it is the dot that indicates the inverter. This dot can be combined with the other logic gate symbols, at either an input or output, to indicate that an inversion happens at that point. For example, if the inverter dot is placed at the output of the AND gate, it means that after the AND operation, the result is inverted. 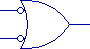(This particular example means the output is "0" when all inputs are "1;" this "not-AND" function is known as a "NAND gate." Placing an inverter at the output of an OR gate is called a "NOR gate.") When you see a dot at any signal on a logic gate, it means that the signal state is inverted at that point. Here are some examples of gates with inverters:

NAND	NOR
Y=NOT(A AND B)	Y=NOT(A OR B)	Y=A AND NOT(B)	Y=NOT(A) OR NOT(B)

It shouldn't be hard to figure out the truth tables for these combined gates. And actually, if you did, you might notice something interesting: the last example has the same truth table as the NAND gate, even though they look nothing alike.

There is a principle called DeMorgan's Theorem which says simply that a logical binary expression remains unchanged if you invert the inputs and outputs and swap ANDs and ORs. That is, for any gate, if you invert a signal which wasn't inverted, and take away the inverters that were there, and also change any AND into an OR and any OR into an AND... the truth table comes out the same. If this doesn't seem intuitive to you, try a few more truth tables until you believe that it always works.

Think about our description of the AND gate. "For the output to be '1,' you need a '1' at both input A and input B." But we would be just as correct to say: "For the output to be '0', you need a '0' at input A or input B." That's consistent with DeMorgan's theorem. And really, we may not always think of our logic in terms of "1" being the "active" state. When we do so we are using "positive logic," but there can be other times when we are more interested in the 0s than in the 1s. We will encounter signals in computer electronics which are called "active low," which means that "0" represents a state we care most about.

Next: Registers

Previous: Binary

Copyright ©2003-2006, Mark Bereit. All rights reserved.